Définition d'un Mot ou d'un Terme du cours

Le carré du nombre \(x\) est égal \(x×x\) qu'on écrit aussi \(x^2\).

Il se trouve que la surface d'un carré dont un côté est de longueur \(x\) vaut \(x^2\).

Donc un nombre au carré peut être représenté par la figure d'un carré dont le côté sera d'une longueur égale à ce nombre.
Un bon petit dessin et vous le verrez bien !

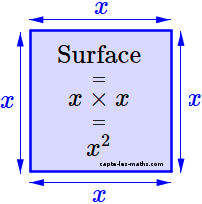
Un carré a tous ses côtés égaux.
Sur la figure nous leur donnons la longueur \(x\)
La surface est donc égale à \(x×x\)
Nous visualisons ainsi le nombre \(x^2\)
C'est le côté du carré à la puissance \(2\)

Et n'allez pas penser que tout ça on s'en fiche un peu. Non ! C'est toujours bien de visualiser une notion, on la retient mieux !

Le mot racine désigne ce qui se trouve à l'origine, au début, à la source, au fondement... De ce point de vue, le côté d'un carré est ce qui le définit le mieux, ce qui en est l'origine. C'est lui qui permet de calculer la surface du carré dont il est le côté. On pourrait presque affirmer que le côté est la « racine du carré ».

La racine carrée de la surface d'un carré est égale à la longueur du côté de ce carré.

Ce qui reste une phrase un peu compliquée !

Ce qui nous intéresse ici ce sont les nombres. Prenons un carré de longueur de côté égale à \(3\), sa surface est donc égale à \(3×3\), soit \(3^2\).

Nous voyons donc que la racine carrée d'un carré de surface \(3^2\) est égale à \(3\) :

racine carrée de \(3^2=3\)

Nous constatons que \(3\) se retrouve dans les deux membres.

La racine carrée d'un nombre ( ici \(9\) ) est le nombre ( ici \(3\) ) dont le carré est égal au nombre donné ( c'est à dire \(9\) qui vaut \(3^2\) ).

Nous voyons que le lien entre un carré et sa racine est étroit. Une fois cette relation bien comprise le reste ne sera qu'affaire de mémoire et de technique de calcul.

Nous savons élever au carré un nombre : \(3\longmapsto3^2=9\)

Nous avons compris ce que veut dire racine d'un nombre : \(9=3^2\longmapsto3\)

Elever au carré et prendre la racine carrée sont des fonctions réciproques, c'est à dire qu'en les appliquant l'une après l'autre on revient au nombre initial.

Constatons-le avec notre exemple numérique :

\[3\xrightarrow{\text{puissance 2}}9\xrightarrow{\text{racine carree}}3\]

Et :

\[9\xrightarrow{\text{racine carree}}3\xrightarrow{\text{puissance 2}}9\]

Nous allons voir que nous pouvons écrire cette relation entre le carré et la racine sous forme de formule mathématique.

La racine carrée de \(4\) se note \(\sqrt4\) et se lit racine de 4 ou racine carrée de 4.

La barre horizontale recouvre toute l'expression dont on doit prendre la racine carrée : \(\sqrt{157×12+5}\)

Il est possible de calculer la racine de \(4\) (donc écrire \(\sqrt4\)), mais pas la racine carrée de \(-4\) (on ne peut pas écrire \(\require{cancel}\cancel{\sqrt{-4}}\)).

Calculer une racine carrée, c'est répondre à une petite énigme : quel est le nombre qui, élevé au carré, donne la valeur qui est sous le radical ?

Tout s'éclaircit avec un exemple !

En reprenant exactement la définition, nous voyons que nous cherchons un nombre \(a\) tel que \(a^2=4\) (\(4\) jouant ici le rôle du \(x\))

Ce \(a\) que nous cherchons est le nombre qui élevé au carré a pour résultat \(4\)

Sans faire durer le suspense, nous savons bien que \(4=2^2\)

Le nombre \(a\) est donc égal à \(2\) et nous pouvons dire que la racine carrée de \(4\) est \(2\)

En utilisant le symbole de la racine carrée nous écrivons, \(\sqrt4 = 2\)

1. Nous commençons par une règle impérative :

   

   Une racine carrée est un nombre positif, autrement dit si on effectue le calcul d'une racine carrée, le résultat de l'opération sera \(\geqslant0\).

   ---

2. De l'équation définition nous pouvons déduire que : \[\boxed{(\sqrt x)^2=x\;\;\;\;\small{\mathbf{si}}\normalsize\;x\geqslant 0}\]

   Une petite démonstration au cas où...

   Pour \(x\geqslant 0\) et \(a^2=x\) nous avons : \(\sqrt x=a\)
   Nous élevons les deux membres à la puissance 2 : \((\sqrt x)^2=a^2\)
   Nous reprenons la condition \(a^2=x\) et nous obtenons : \((\sqrt x)^2=x\)

   Nous voyons ici que \(\sqrt x\) est racine, c'est à dire solution, d'une équation de la forme \(y^2=k\) (voir ici pour approfondir ces problèmes d'équations).

   Nous retrouvons l'idée que carré et racine sont des fonctions réciproques. Nous pouvons maintenant écrire leur lien sous une forme plus mathématique en reprenant l'exemple de \(9\) : \[(\sqrt9)^2=9\] En appliquant à \(9\) la fonction racine, puis la fonction puissance \(2\) au résultat, nous retrouvons le point de départ, c'est à dire \(9\).

   ---

3. La propriété suivante traduit simplement la phrase : la racine du nombre \(x\) élevé au carré est ce nombre \(x\) lui-même.

   \[\boxed{\sqrt{x^2} = x\;\;\;\;\small{\mathbf{si}}\normalsize\;x\geqslant 0}\]

   Dans cette formule, voici encore nos fonctions réciproques en action. Nous appliquons à \(3\) la fonction puissance \(2\) puis au résultat la fonction racine : \[\sqrt{3^2}=3\] Et nous retrouvons \(3\) !

   ---

4. Il peut être intéressant de savoir que \[\boxed{\sqrt x=x^\frac12}\] ça peut servir avec Excel ou GeoGebra ou...

   ---

5. L'équation du second degré \(\,y^2=k\) (\(k\) est un nombre positif) admet deux solutions :

   • \(y=\sqrt k\) où \(y\) sera un nombre positif
   • \(y=-\sqrt k\) où \(y\) sera un nombre négatif

   En effet :

   \[\begin{align} y^2 & = (\sqrt k)^2 \\ & = k \end{align}\]

   Ou :

   \[\begin{align} y^2 & = (-\sqrt k)^2 \\ & = (-\sqrt k) × (-\sqrt k) \\ & = (\sqrt k)^2 \\ & = k \end{align}\]

   L'équation \(y^2=11\) a pour solutions \(y=\sqrt{11}\) et \(y=-\sqrt{11}\)

   La démonstration de cette équation, un grand classique de la classe de troisième, est assez simple en utilisant une identité remarquable. En effet l'équation \(y^2=k\) peut s'écrire \(y^2-k=0\). De plus rappelons nous bien que \(k\) est un nombre positif.

   Nous avons une différence de deux nombres au carré, ce qui correspond à l'égalité remarquable \(A^2-B^2=(A-B)(A+B)\).

   Donc notre équation se transforme en un produit de facteurs : \(y^2-k=(y-\sqrt k)(y+\sqrt k)=0\)

   Un produit de facteurs est nul si l'un des facteurs l'est, et cela se produit pour \(y=\sqrt k\) ou \(y=-\sqrt k\).

Il faut connaître par coeur les carrés des premiers entiers, cela vous aidera à résoudre les exercices.

Le calcul des racines de \(0,1,4,9\) donne un nombre entier :

Le calcul des racines des nombres entiers \(2,3,5,6,7,8\) ne donne pas un résultat entier :

\(\sqrt2,\sqrt3,\sqrt5,\sqrt7\) ne peuvent pas se calculer d'une façon exacte et sauf si on si on vous le demande, laissez-les avec le radical.

Mais les entiers \(6\) et \(8\) sont un cas particulier :

Les racines \(\sqrt6\) et \(\sqrt8\) peuvent se simplifier. Nous vous donnerons leur décomposition en vous expliquant comment réduire des expressions comprenant des racines carrées.

Là nous avons une contrainte impérative, b doit être différent de zéro (nous savons bien qu'il n'est pas possible de diviser par 0...)

Nous pouvons multiplier et diviser des racines carrées, mais - malheureusement - il n'existe pas le même genre de formules pour l'addition et pour la soustraction...

Pour les simplifier, nous devons décomposer les expressions pour faire apparaître des carrés parfaits et ne conserver sous forme de racine que les termes dont le calcul ne donnerait pas un nombre entier.

Dans un premier temps, étudions les exemples de \(6\) et de \(8\).

Nous pouvons décomposer \(6\) en produit des entiers \(2\) et \(3\) : \[6=2×3\] Donc \[\sqrt6=\sqrt{2×3}\] En appliquant la propriété des produits de racines carrées : \[\sqrt6=\sqrt2×\sqrt3\]

Nous avons là la simplification ultime de l'expression, aller plus loin serait effectuer le calcul.

De la même façon \(8\) est le produit de \(2\) et \(4\)

\[\begin{align} \sqrt8 & =\sqrt{2×4} \\ & =\sqrt2×\sqrt{2^2} \\ & =\sqrt2×2 \\ & =2\sqrt2 \end{align}\]

Nous sommes au bout du calcul !

Une suite d'opérations sur les racines carrées est un peu décourageante à regarder, l'oeil ne sait pas trop où se fixer. Ce n'est qu'une impression : prenez-le temps de dérouler les calculs ligne à ligne, ou encore mieux de les réécrire. La mécanique du calcul se révèlera à vous...

Deux petits exercices vont nous le montrer...

La première étape consiste à décomposer chaque nombre en produit de facteurs, en séparant les facteurs irréductibles et ceux qui sont des carrés parfaits.

\[\sqrt{20}+\sqrt{45} = \sqrt{4×5}+\sqrt{9×5}\]

Nous appliquons ensuite la règle de multiplication des racines carrées que nous venons de vous donner

\[\sqrt4×\sqrt5+\sqrt9×\sqrt5\]

Pour bien comprendre, nous faisons apparaître les carrés parfaits

\[\sqrt{2^2}×\sqrt5+\sqrt{3^2}×\sqrt5\]

Nous effectuons le calcul des racines carrées

\[2×\sqrt5+3×\sqrt5\]

Nous factorisons le facteur commun (voir ce qu'est la factorisation).

\[(2+3)\sqrt5\]

Nous effectuons l'addition

\[5\sqrt5\]

Donc l'expression \(\sqrt{20}+\sqrt{45}\) simplifiée est égale à \(5\sqrt5\)

Dans \(5\sqrt5\) , le \(×\) est implicite car il est inutile d'écrire \(2×\sqrt5\) (cf. ce rappel sur les multiplications implicites dans les équations).

Le résultat du calcul de la racine carrée d'un nombre est rarement un nombre entier. C'est le cas de la racine carrée de 5. Il est plus simple et plus juste (sauf si on vous le demande) de laisser \(\sqrt5\) plutôt que le \(2,23606798...\) que votre machine à calculer se fait un plaisir de vous fournir.

Avec la soustraction, la méthode est exactement la même !

\(\begin{align} \sqrt{20}−\sqrt{45} & = \sqrt{4×5}−\sqrt{9×5} \\ & = \sqrt4×\sqrt5−\sqrt9×\sqrt5 \\ & = 2×\sqrt5−3×\sqrt5 \\ & = (2−3)\sqrt5 \\ & = −\sqrt5 \\ \end{align}\)

L'extraction d'une racine carrée, le calcul en fait, est une opération qui demande de la patience. Le résultat est en général un nombre sans fin (irrationnel), on ne peut pas avoir un résultat exact.

Il existe plusieurs méthodes pour extraire une racine carrée :

• La plus simple et la plus rapide est bien sûr la machine à calculer.

• Mais il existe des approches manuelles que vous pourrez étudier sur ces sites :

  • Pour extraire une racine carrée comme autrefois, avant les calculettes

  • Pour obtenir une valeur approchée de la racine carrée